Continuous Chromogenic Assay for Tissue Factor, Factor VII, or Factor X.
Kosow, Furie, and Forastieri (1974) coupled activation of factor X by Russells viper venom (reaction (A)) to cleavage of a factor Xa-specific chromogenic substrate (reaction (B)). The rate at which P was generated could be described by equation [1], which is the same as the equation for distance traveled over time with initial velocity and constant acceleration.
(A) RVV + X <=> RVV.X --> RVV + Xa
(B) Xa + S --> P
[1] p = v0 ∙ t + ½ ∙ a ∙ t2
It is easy to measure P generated over time t in reaction (B) since P absorbs light with 405nm wavelength. dp/dt can be empirically calibrated, by running a dose-response analysis, to either the RVV or X in reaction (A).
If tissue factor (TF) is allowed to equilibrate with factor VIIa to form the active TF.VIIa complex (C1), then equation [1] should also serve to model the consecutive reactions (C2) and (D).
(C1) TF + VIIa <=> TF.VIIa
(C2) TF.VIIa + X <=> TF.VIIa.X --> TF.VIIa + Xa
(D) Xa + S --> P
To achieve a reliable, standardizable, and sensitive kinetics-based assay for tissue factor functional activity, TF must be the limiting component in reactions (C1) and (C2). If this condition is met, while concentrations of X and S ([X] and [S]) remain much greater than concentrations of Xa and P ([Xa] and [P]), respectively, then
[2] v1 = d[Xa]/dt
= kcat ∙ [TF.VIIa] ∙ [X] / (K + [X]) < K is apparent Km for reaction (C2)>
[3] v2 = d[P]/dt
= k ∙ [Xa] ∙ [S] / (Km + [S])
Intermediate steps provided in Carson (1985) lead to
[4] [P] = k ∙ v1 ∙ [S] ∙ t2 / (2 ∙ (Km + [S] ))
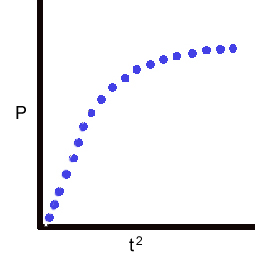 A plot of P vs t2 using only the initial linear points
A plot of P vs t2 using only the initial linear points
(where X>>Xa and S >> P) gives a line (mouse over graph) with
[5] slope = v1 ∙ k ∙ [S] / (2 ∙ (Km + [S] ))
which can be rearranged to solve for v1
[6] v1 = slope / {k ∙ [S] / (2 ∙ (Km + [S] ))}
Since [S] (approximately the starting concentration as long as S>>P), k, and Km are known (Bock et al, 1989), v1 returns [fXa]/min. When calibrated against a TF standard (either as A405nm/min2 vs. TF or fXa/min vs. TF), this assay is capable of quantitating attomoles of functional TF (Carson, 1987).
The current implementation of the RateFit program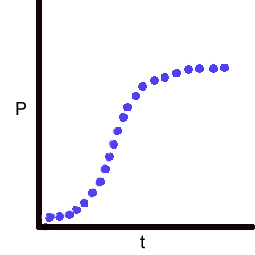
uses a multiple regression algorithm to fit equation [4]
directly to the parabolic portion of the data (mouse over graph).
v1 is solved from
[7] d2[P] / dt2 = v1 ∙ k ∙ [S] / (Km + [S])
Current assay implementation and typical conditions are described in the
appendix in (Carson, 1996).
==============
The assay has been used in multiple projects. Examples include:
Measured TF activity on living cells grown in 96-well plates and in lysates from disrupted cells (Carson and Archer, 1986)
Validated against clot-based assays (Carson, 1987)
Measured induced TF expression on blood monocytes (Brozna and Carson, 1988)
Detected changes in TF activity in response to antibody-mediated complement attack on the cell membrane (Carson and Johnson, 1990)
Determined the degree to which TF activity was de-encrypted in membrane microparticles shed from cultured cells (Carson and Bromberg, 2000).
By changing the reaction conditions so the new analyte becomes limiting (reactions C1, C2 and D), the assay has been used to measure concentrations of fVIIa synthesized by hepatocytes that were differentiated in vitro from pluripotent stem cells (Basma et al, 2009; Balasubramanian et al, 2009).